A lineáris regresszió-analízis
Használata akkor indokolt, ha független változók együttes, lineáris kapcsolatára vagyunk kíváncsiak egyetlen függő változóval.
Feltételek:
Mind a független, mind a függő változóknak normális eloszlásúnak kell lenniük, valamint folytonos változóknak és lehetőség szerint varianciájuk is homogén legyen.
A regresszió-analízist gyakran szokták a korreláció-analízissel együtt emlegetni, hiszen az utóbbinak mintegy kiterjesztése a regresszió-analízis.
A függő és független változók közötti kapcsolat megállapításához az analízis a legkisebb négyzetek módszerének segítségével egy egyenes egyenletét írja fel, mely a következőképpen néz ki:
Y = b1*x1 + b2*x2 + c + e
Ahol Y a függő változó értéke, b
n a független változók együtthatója, c a konstans, míg e a hiba mértéke, mely a regresszió-egyenestől való eltérést mutatja.A regresszió-analízis menete.
Milyen összefüggés állapítható meg az életkor és a szorongás mértéke között, melynek vizsgálatához 15 fővel felvettünk egy szorongás kérdőí
vet, és regisztráltuk életkorukat.Az adatok bevitele után kiválasztjuk az analyze menüből a “regression” almenüt, azon belül pedig a “linear…” pontot.

Az eredmények a következők:
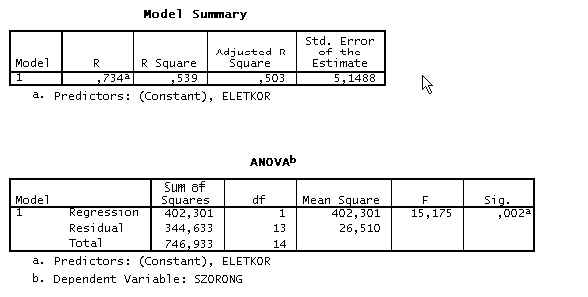
A modell alapján megállapítható összefüggések véletlennél nagyobb valószínűségéről az ANOVA táblázat szignifikancia-értéke ad tájékoztatást.
Az itt található szignifikancia-érték, nemcsak a regresszió-egyenes által megállapított kacsolat érvényességét mutatja meg, hanem a determinációs együtthatóét (R square),illetve ennek módosított (adjusted R square) változatáét is.
A determinációs együttható a független és függő változó közös varianciájának százalékát mutatja. Jelen esetben ez az érték 0.503, vagyis az életkor és a szorongás varianciája kb. 50%-ban megegyezik.
A kapcsolat szorosságára vonatkozó további számadatok közül a több független változó hatásának összehasonlítására szolgáló B és ennek sztandardizált változata a “b ” mutatja meg a szóban forgó független változó együtthatóját.
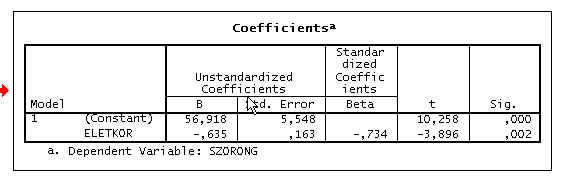
A “B érték” a függő változó átlagos növekedését mutatja meg, ha a szóban forgó független változó értéke 1-gyel növekszik. A “standardized Coefficients Beta” pedig a függő változó szórásának átlagos változását adja meg a független változó szórásváltozásának egységnyi növekedésének függvényéb
en.Ebben a táblázatban jelenik meg a független változó (nem a modell!!!) hatására vonatkozó szignifikancia-érték. Ha ez 0.05-nél kisebb, a független változónak nincs jelentős hatása a függő változóra.
Több független változó esetén a “beta” értékek összehasonlításával lehet meghatározni, melyiknek van nagyobb hatása a függő változóra. A “Beta” érték adja meg az összefüggés irányát is.
Összefoglalva, az életkor és a szorongás között jelentős összefüggés állapítható meg a regresszió-analízis segítségével (F(1, 14)=15,175; p<0,05). Az összefüggés iránya negatív, vagyis minél idősebb a mintában szereplő személy, annál alacsonyabb szorongásértékkel rendelkezik az adott kérdőív alapján.
Logisztikus regresszió
Használata akkor javasolt, ha a függő változó kategori
kus változó, vagyis csak két, esetleg három értékkel bír (lehet több is, de az eredmények interpretálását nehezebbé teszi, ha több csoport van).Segítségével analóg megállapítások tehetők, függő és független változó között, mint a lineáris regresszió eseté
ben.Kérdésünk az, hogy a szívbetegség és a szorongás mértéke (melyet egy szorongás kérdőív alapján állapítottunk meg) között kimutatható-e összefüggés.
Az analízis kiválasztása szintén az analyzeà regression menüben történik, de a binary logistic pontot választjuk ki.
Az eredmények értékelése
A Block 1 eredményeket értelmezzük.
Az omnibus test analóg a lineáris regresszió ANOVA tesztjével. Segítségével megállapítható, hogy a modellben szereplő független változók a véletlennél nagyobb valószínűséggel állnak kapcsolatban a függő változóval.
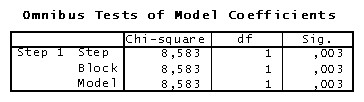
F-próba helyett itt Khi2 próba található. Ennek szignifikancia-értéke kisebb, mint 0,05, tehát a modell szignifikáns összefüggést mutat a független és függő változók között.

Szükségünk van arra is, hogy a változók varianciája közötti kapcsolatot is megállapíthassuk, hasonlóan a determinációs együtthatóhoz. Ezt a feladatot a logisztikus regresszió esetében a “Nagelkerke R square” látja el. Ennek értéke 0,582, tehát a független változó és függő változó varianciája 58,2%-ban megegyezik.
A modell prediktív képessége (mivel a regresszió analízis nemcsak összefüggések megállapítására használható, hanem predikció is tehető vele) a következő táblázatból derül ki:
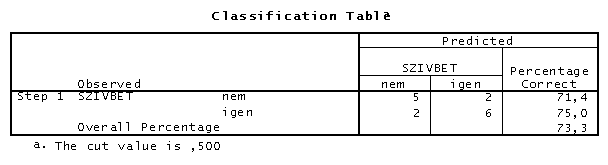
Vannak megfigyelt (observed) és bejósolt (predicted) értékeink. Előbbiek a mintánkban szereplő “szivbet” változó értékei, míg utóbbiak a regressziós összefüggés kiszámítása utáni állapotnak feleltethetőek meg. Minél nagyobb az “overall percentage” érték, annál jobb a modell. Tehát az omnibus teszten kívül figyelembe kell vennünk a modell klasszifikációs tábláját is ahhoz, hogy az összefüggésekről árnyaltabb képet kapjunk.
Marad még egy kérdés: ha több független változónk van, akkor a lineáris regresszió “beta” értékéhez, milyen mutató kapcsolható a logisztikus regresszióban a független változók hatásának összehasonlításához?
A válasz az, úgynevezett “odds ratio” vagy Exp(B).

Két értékű függő változó esetében két lehetőséghez járulhat hozzá a független változó: vagy annak a valószínűségét növeli, hogy a függő változó 1 lesz, vagy azt, hogy 0.
Az Exp(B) értéke megmutatja ezt a valószínűséget, mégpedig úgy, hogy ha Exp(B) értéke 1-nél nagyobb, akkor annak a valószínűségét növeli a független változó, hogy a függő változó értéke 1 lesz. Ha viszont Exp(B) értéke 1-nél kisebb (0 és 1 közötti szám), akkor a függő változó értéke nagyobb valószínűséggel lesz 0, mint 1.
Éppen ezért nagyon fontos, hogy tudjuk, a modellben a függő változó mely értékeit képviseli a 0, és melyeket az 1. Erről tájékoztat a “dependent
variable encoding” táblázat, mely az analízis második táblázata (nem a block 1-en belül).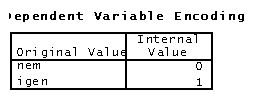
Jelen példánk szerinti értelmezés tehát így hangzik:
A szívbetegség előfordulása és a szorongás mértéke között jelentős összefüggés állapítható meg. Blablabla
A szorongás mértékének növekedése 38%-kal növeli a szívbetegség előfordulásának valószínűségét.