Variancia analízis
Miért nem elég a kétmintás t-próba?
Amikor arra a kérdésre keressük a választ, hogy a mért változó várható értéke megegyezik-e két mintában, az adatokat a kétmintás t-próbával elemezzük. Ennél az egyszerű esetnél gyakrabban fordul elő, hogy kettőnél több csoportot szeretnénk összehasonlítani. Kézenfekvőnek tűnik, hogy ilyenkor is alkalmazzuk a már jól bevált módszert, a kétmintás t-próbát. Mégsem ezt tesszük és erre jó okunk van (kettő is).
Legyen 3 csoportunk (mondjuk A, B és C). Ekkor az A és B, A és C, B és C csoportokat kell összehasonlítani, azaz 3 darab 2 mintást-próbát kellene elvégezni. Több csoport esetén még rosszabb a helyzet ( 4 csoportnál 6, 5 csoportnál már 10, N csoport esetén N×(N-1)÷2). Ez már önmagában is indokolja, hogy nézzünk más megoldás után, amely lehetővé teszi egyetlen próba alkalmazását kettőnél több csoport esetén is
Van még egy indok és ez a fontosabb. Minden próbánál az eredményt valamilyen pontossággal kapjuk, szokásosan az elsőfajú hiba (fenntartjuk a nullhipotézist, azt, hogy a két csoport várható értéke nem különbözik) valószínűsége 0,05. Viszont 3 csoport összehasonlításánál már nem ennyi, hiszen nem egy összehasonlítást végzünk. Precízebben, nem egyszerűen egy P(A) valószínűséggel van dolgunk, hanem a három csoport miatt P(A + B +C) val
ószínűséggel. Ha ez egyszerűen a P(A) + P(B) + P(C) összeg lenne, úgy ez 0,05 + 0,05 + 0,05 = 0,15 vagy 5 csoport esetén 0,25, azaz, bár kétmintás t-próbánként 0,05 a hiba valószínűsége, az összes csoportot tekintve ez már 0,15 (5 csoportnál 0,25). A helyzet még rosszabb, az összefüggés nem ilyen egyszerű, a három csoport esetén szükséges 3 összehasonlításnál 0,142-re, öt csoportnál pedig 0,315-re nőne az elsőfajú hiba.Mi a lényege?
A varianciaanalízis próbák egy csoportját jelenti, melyeket kettőnél több csoport vagy kettőnél több változó esetén alkalmazunk. Ennek megfelelően lehet független mintás vagy összetartozó mintás, illetve egy szempontos vagy több szempontos varianciaanalízis.
Az alapelv a teljes variancia felbontása. Pl. egy szempontos független mintás VA esetén a teljes varianciát egy belső (csoporton belüli) ill. egy külső (csoportok közötti) varianciára bontjuk. A belső variancia a csoportokon belüli változékonyságot méri, azaz mintavételi hibának tekinthető, a külső variancia pedig a csoportok közötti változékonyságot méri, ami szintén mintavételi hiba vagy a független változó hatása. Ha a független változó nincs hatással a függő változóra, akkor a külső variancia megegyezik a belső varianciával. Ha viszont a független változó hat a függő változóra, akkor a külső variancia nagyobb, mint a belső variancia. A két variancia hányadosa egy F értéket ad, amely annál nagyobb, minél nagyobb a külső variancia. A kiszámolt F értékről az F eloszlás alapján meg tudjuk mondani, hogy valószínűsége 0,05 alatt van-e, ami nyílván akkor teljesül, ha a független változó hatással van a függő változóra, azaz a külső variancia jóval nagyobb, mint a belső. Kicsit formálisabban, a varianciák helyett csak az átlagtól való eltéréseket nézve,
X –Xteljes átlag = (X – Xcsoport átlag) + (Xcsoport átlag – Xteljes átlag )
Teljes Belső Külső
Többszörös összehasonlítás
A varianciaanalízis csak azt mutatja meg, hogy a csoportok különböznek-e, de azt nem, hogy a különbséget mi okozza – pl. 5csoport esetén lehet, hogy csak az első különbözik a negyediktől, a többi egyforma, de az is lehet, hogy mindegyik csoport mindegyiktől különböző. Ezért szükség van egy olyan módszerre, amelyik megmutatja, mi vagy mik okozzák a szignifikáns különbséget a csoport átlagokban. Ez a többszörös összehasonlítás, ami formailag hasonlít a t-próbára, csak kicsit másként kell számolni!
Alkalmazhatóság
Két feltételnek kell teljesülnie a VA alkalmazhatóságához.
Az adatok normalitása – elég nagy minta elemszámnál már teljesül.
A csoportok, minták szórása ne különbözzön szignifikánsan – ha ez nem teljesül, akkor a korrigált eljárást (pl. Greenhaus – Geiser) kell használni.
Egyszempontos variancia analízis független minták esetén
Ezt az eljárást alkalmazzuk akkor, ha kettőnél több csoportot szeretnénk összehasonlítani egy változó mentén, pl. az alvásidőt nézzük a populációból vett mintán, amely 3 csoportból áll: gyerekek, felnőttek, idősek vagy egy másik pl. az intelligenciahányados tekintetében okoz-e különbözőséget az eltérő iskolai végzettség (általános-, közép, felsőfokú).
Adatbevitel
Minden egyes személy két adattal rendelkezik, az egyik az, amit mértünk, a másik pedig az, hogy melyik csoportba tartozik. Ennek megfelelően két oszlopba kerülnek az adatok, az egyik oszlop tartalmazza a csoportosító változó értékeit, a másik a mért értékeket. A személyek adatait egymás alá (a sorokba) kell beírni pl. úgy, hogy az első oszlopba kerül a csoport azonosító értéke, a másodikba a mért érték.
Példa:
Két hormonkészítmény depresszióra való hatását szeretnénk megvizsgálni. Ehhez 3 csoportot képezünk, az egyik a kontroll csoport, akik placebot kapnak a második csoport az egyik, a harmadik csoport a másik készítményt kapja. A kezelések után egy skálán bemérjük a depresszió mértékét. A független változó a csoport, a függő változó a depresszió mértéke. Van-e hatása a drognak? (valóban függ-e depresszió mértéke a különböző csoportokban?)
Az adatok:
|
Egyik hormon (csoport 1) |
Másik hormon (csoport 2) |
Placebo (csoport 3) |
|
9 |
4 |
3 |
|
12 |
2 |
6 |
|
8 |
5 |
3 |
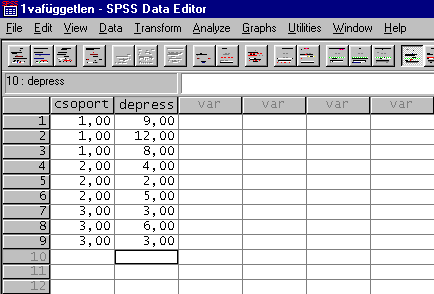
Első lépésként írjuk be az adatokat a szerkesztőbe:
A “csoport” nevű változó tartalmazza a csoportosító adatokat, a “depress” pedig a depresszió mértékét.

Ezután indítsuk el az Analyze menűből aCompare Means almenű One-Way ANOVA.. p
rogramját.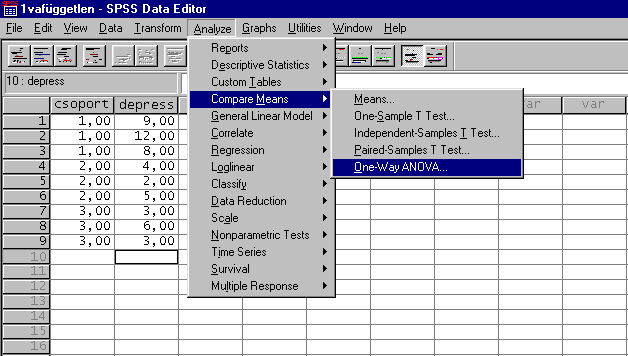
A megjelenő ablak bal oldalán találhatóak a változók nevei. Mivel a “depress” a függő változó, a depress változóra kattintunk majd a mellette levő nyílra ( u
), a Dependent List: ablakba ekkor megjelenik a depress. A független változó (faktor) a csoport, ezért a “csoport” változót a Factor ablakba “küldjük (kattintás a csoport-ra majd a u -ra.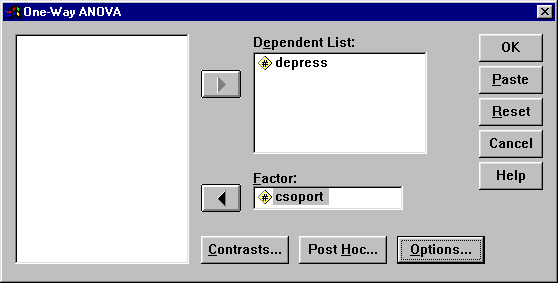
Ezzel készen is van az alapbeállítás, most jöhet a finomítás. Az Options… - ra kattintva beállíthatók a különböző lehetőségek.
A Descriptive bejelölésével a program kiírja az alap statisztikai adatokat (átlag, szórás, stb).
A Homogeneity-of-variance elvégzi a szórások homogenitásának vizsgálatát.
A Means plot az átlagokból egy grafikont készít.
A Missing Values a hiányzó adatok kezelését teszi lehetővé
Exclude cases analysis by analysis – kihagyja az elemzésből azokat az eseteket, ahol hiányzó adat van azokban a változókban, amelyeket ebben a varianciaanalízisben használ
Exclude cases listwise – kihagyja azokat az eseteket, ahol bármely változóban van hiányzó adat, ez ebben a feladatban nem lehetséges, de összetettebb vizsgálatokban érdekes lehet, hogy csak azoknak a személyeknek az adatait használjuk, akiknek van érvényes adata az összes többi változóban is.
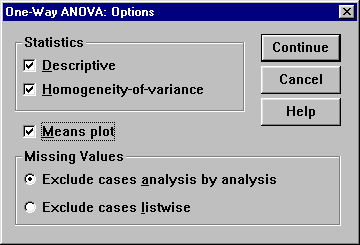
Ha készen van " Continue és visszajön a One-way Anova ablak. Most a Post-Hoc almenű következik, ahol meg lehet adni, hogy készüljön-e vagy sem többszörös összehasonlítás. Erre kattintva megjelenik egy újabb ablak, ahol megadható, hogy azonos varianciák (Equal Variances Assumed) ill. nem azonos varianciák (Equal Variances Not Assumed) esetén melyik módszer szerint készüljön a többszörös összehasonlítás
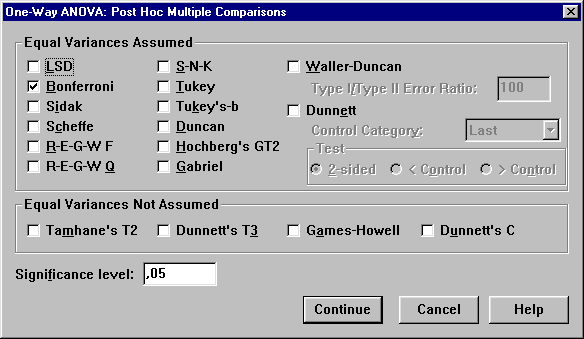
Ha készen van " Continue és visszajön a One-way Anova ablak. Itt az OK – ra kattintva elindul az elemzés, majd megjelenik egy új képernyő, amelyen az eredmények láthatóak.
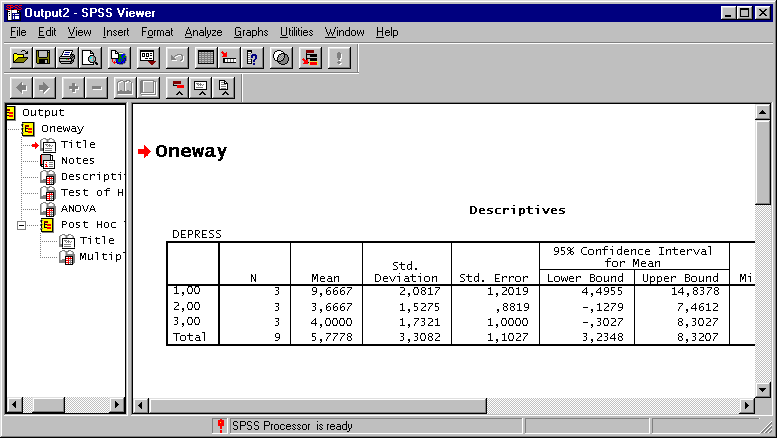
Mivel kértük, megjelennek a statisztikai alapadatok (Descriptives).
Descriptives
DEPRESS
|
|
N |
Mean |
Std. Deviation |
Std. Error |
95% Confidence Interval for Mean |
|
Minimum |
Maximum |
|
|
|
|
|
|
Lower Bound |
Upper Bound |
|
|
|
1,00 |
3 |
9,6667 |
2,0817 |
1,2019 |
4,4955 |
14,8378 |
8,00 |
12,00 |
|
2,00 |
3 |
3,6667 |
1,5275 |
,8819 |
-,1279 |
7,4612 |
2,00 |
5,00 |
|
3,00 |
3 |
4,0000 |
1,7321 |
1,0000 |
-,3027 |
8,3027 |
3,00 |
6,00 |
|
Total |
9 |
5,7778 |
3,3082 |
1,1027 |
3,2348 |
8,3207 |
2,00 |
12,00 |
Ezután következik a szórások homogenitásának vizsgálata (mert bejelöltük).
Test of Homogeneity of Variances
DEPRESS
|
Levene Statistic |
df1 |
df2 |
Sig. |
|
,293 |
2 |
6 |
,756 |
Az eredmény: nem szignifikáns mert Sig. 0,756, azaz csoportok a szórás tekintetében homogének. Jöhet a varianciaanalízis.
ANOVA
DEPRESS
|
|
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Between Groups |
68,222 |
2 |
34,111 |
10,586 |
,011 |
|
Within Groups |
19,333 |
6 |
3,222 |
|
|
|
Total |
87,556 |
8 |
|
|
|
A csoportok közötti különbség szignifikáns - F(2,6)=10,58 p<0,05
Azt, hogy mi okozza a szignifikáns különbséget, a többszörös összehasonlítás (Multiple Comparisons) mutatja meg:
Multiple Comparisons
Dependent Variable: DEPRESS
Bonferroni
|
|
|
Mean Difference (I-J) |
Std. Error |
Sig. |
95% Confidence Interval |
|
|
(I) CSOPORT |
(J) CSOPORT |
|
|
|
Lower Bound |
Upper Bound |
|
1,00 |
2,00 |
6,0000* |
1,4657 |
,019 |
1,1817 |
10,8183 |
|
|
3,00 |
5,6667* |
1,4657 |
,025 |
,8484 |
10,4849 |
|
2,00 |
1,00 |
-6,0000* |
1,4657 |
,019 |
-10,8183 |
-1,1817 |
|
|
3,00 |
-,3333 |
1,4657 |
1,000 |
-5,1516 |
4,4849 |
|
3,00 |
1,00 |
-5,6667* |
1,4657 |
,025 |
-10,4849 |
-,8484 |
|
|
2,00 |
,3333 |
1,4657 |
1,000 |
-4,4849 |
5,1516 |
* The mean difference is significant at the .05 level.
A táblázatban a Mean Difference oszlopban * jelzi, hogy mely esetben van szignifikáns különbség 0,05 szinten, bár ez a Sig. Oszlop értekei alapján is leolvasható.
Esetünkben az látható, hogy az 1-es csoport különbözik a 2-es és a 3-as csoporttól és nincs más különbség.
Az utolsó, amit beállítottunk, az ábra. Ez egyszerűen a csoport átlagokat rajzolja meg. Az eredmény alapján már tudjuk, hogy ez valójában torzít, mert a 2 és 3 közötti emelkedés csak a véletlen műve.
Means Plots
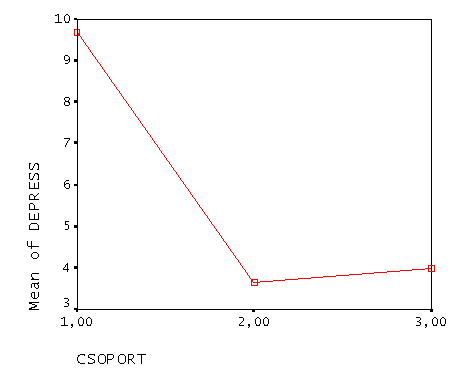
Az eredmény megadása
A három csoport a depresszió tekintetében szignifikánsan különbözik – F(2,6)=10,58 p<0,05. A különbséget a Bonferroni féle többszörös összehasonlítás szerint az okozza, hogy az 1 hormont kapott csoport különbözik a másik két csoporttól, melyek viszont nem különböznek egymástól. Az 1 jelű hormon hat a depresszióra, a 2 jelű nem (ez a mondat az, amiért a vizsgálatot és a statisztikát megcsináltuk).
Egy szempontos variancia analízis összetartozó minták esetén
Ezt az eljárást alkalmazzuk akkor, ha egy csoportot vizsgálunk kettőnél t
öbb helyzetben.Adatbevitel
Az adatokat úgy kell beírni, hogy a sorokban szerepeljenek az egyes személyek adatai, az oszlopokban pedig a változó szintjei.
Példa
Donders additiv modelljének ellenőrzésére hallgatók egy 10 fős csoportjával egyszerű-, szelektív- és választásos reakcióidő feladatokat végeztünk. Az adatok:
ERI SRI VRI
140 180 180
180 220 210
160 170 220
210 190 250
240 270 310
190 210 240
210 230 270
170 210 250
200 240 280
150 190 240
Ha kész az adatbevitel, akkor az eljárás a következő:
Analyze
General Linear Model
Repeated Measures
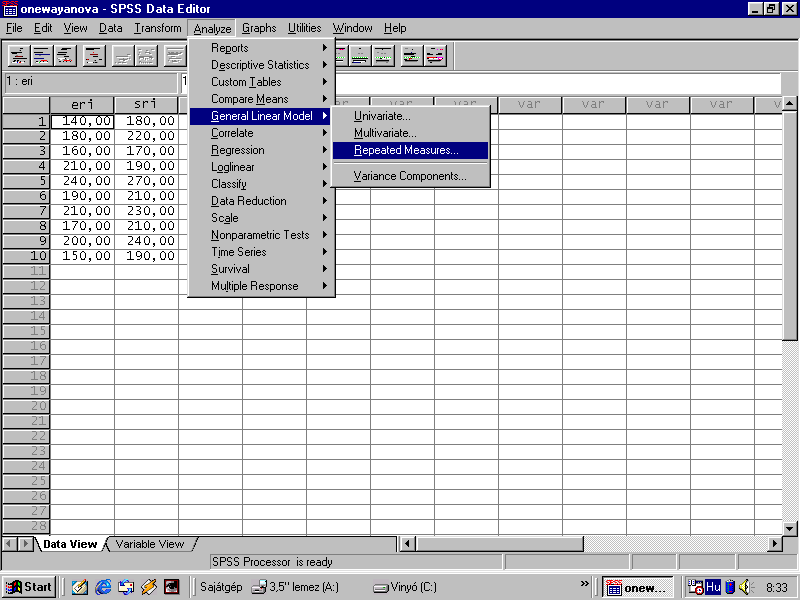
Megjelenik az alábbi ablak, ahol a “Within-Subject Factor Name:” ablakba lehet beírni a vizsgált változó nevét (nem kötelező, ekkor a gép által adott “factor1” lesz a név). A következő lépés a szintek megadása a Number of Levels: ablakban. Mivel a reakcióidő 3 szintjét mértük (egyszerű-, szelektív- ls választásos RI) ezért ide 3-at kell írni és rákattintani az “Add” gombra.
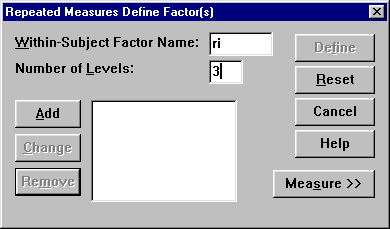
Ha készen van, akkor " Measure. A megjelenő ablak tekinthető a főmenűnek, itt kell beállítani az összes fontosabb paramétert.
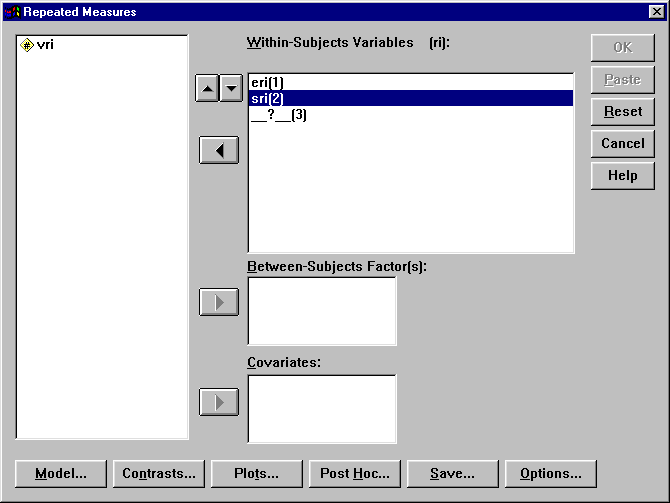
A bal oldali ablakban láthatók a szintek nevei, ezekre egyenként rákattintva a u gombbal berakjuk őket a Within-Subjects Variables ablakba.
Most jöhet au Options menü.
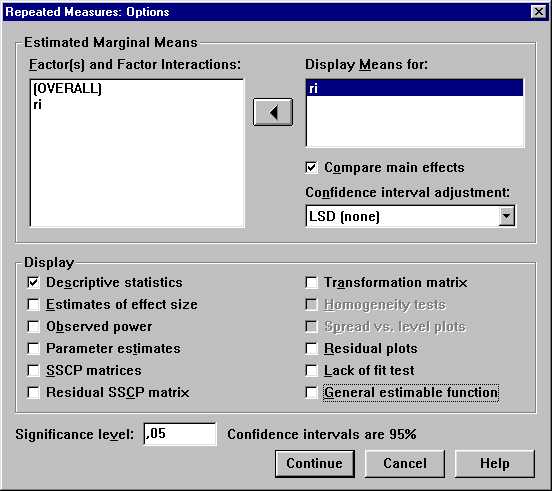
A minta szerint érdemes bejelölni a lehetőségeket, az eddigiek alapján az értelmezésük már nem lehet nehéz. Fontos! A Diplay Means for: ablakba be kell tenni a változó nevét, különben nem kérhető a compare main effects.
A Continue után visszatérünk a “főmenűbe”, ahol a Plots-ra érdemes kattintani.
A megjelenő ablakban a minta szerint betesszük a változót (katttintás a Factors ablkaban levő ri-re majd a Horizontal Axis: melletti u
-re, majd a Plots: melletti Add-ra).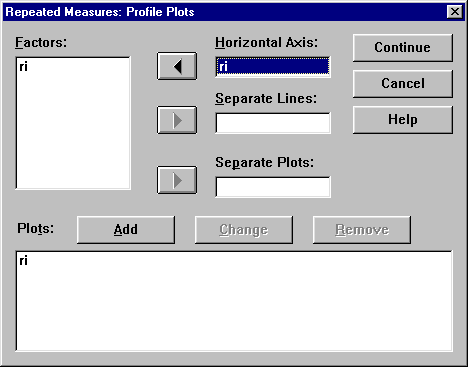
A Continue után visszatérünk a főmenübe, ahol az OK-ra kattintva a program
lefut. Megjelenik egy újabb ablak az eredményekkel.
Először az alapstatisztikákat vehetjük szemügyre :
Descriptive Statistics
|
|
Mean |
Std. Deviation |
N |
|
ERI |
185,0000 |
31,0018 |
10 |
|
SRI |
211,0000 |
30,3498 |
10 |
|
VRI |
245,0000 |
36,8932 |
10 |
Ezután egy olyan erdmény jelenik meg ami az utána kvetkező varianciaanalízis táblázat értelmezéséhez kell. Azt kell megnézni, hogy szignifikáns-e (Sig. Oszlop, most 0,901).
Mauchly's Test of Sphericity
Measure: MEASURE_1
|
|
Mauchly's W |
Approx. Chi-Square |
df |
Sig. |
Epsilon |
|
|
|
Within Subjects Effect |
|
|
|
|
Greenhouse-Geisser |
Huynh-Feldt |
Lower-bound |
|
RI |
,974 |
,213 |
2 |
,901 |
,974 |
1,000 |
,500 |
Tests the null hypothesis that the error covariance matrix of the orthonormalized transformed dependent variables is proportional to an identity matrix.
a May be used to adjust the degrees of freedom for the averaged tests of significance. Corrected tests are displayed in the Tests of Within-Subjects Effects table.
b Design: Intercept Within Subjects Design: RI
Az alábbi táblázat mutatja a varianciaanalízis eredményeit. Most az RI melletti sort kell nézni, egyrészt mert RI a változónk neve másrészt, mert a szférikusság teszt eredménye nem szignifikáns, tehát a Sphericity Assumed sort. Az F=42,58 és a Sig. Oszlopból látszik, hogy p< 0,05 tehát szignifikánsan különböznek az átlagok. Azt, hogy ezt mi okozza, a következő táblázat mutatja meg.
Tests of Within-Subjects Effects
Measure: MEASURE_1
|
Source |
|
Type III Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
RI |
Sphericity Assumed |
18106,667 |
2 |
9053,333 |
42,585 |
,000 |
|
|
Greenhouse-Geisser |
18106,667 |
1,949 |
9291,183 |
42,585 |
,000 |
|
|
Huynh-Feldt |
18106,667 |
2,000 |
9053,333 |
42,585 |
,000 |
|
|
Lower-bound |
18106,667 |
1,000 |
18106,667 |
42,585 |
,000 |
|
Error(RI) |
Sphericity Assumed |
3826,667 |
18 |
212,593 |
|
|
|
|
Greenhouse-Geisser |
3826,667 |
17,539 |
218,178 |
|
|
|
|
Huynh-Feldt |
3826,667 |
18,000 |
212,593 |
|
|
|
|
Lower-bound |
3826,667 |
9,000 |
425,185 |
|
|
Pairwise Comparisons
Measure: MEASURE_1
|
|
|
Mean Difference (I-J) |
Std. Error |
Sig. |
95% Confidence Interval for Difference |
|
|
(I) RI |
(J) RI |
|
|
|
Lower Bound |
Upper Bound |
|
1 |
2 |
-26,000 |
6,182 |
,002 |
-39,986 |
-12,014 |
|
|
3 |
-60,000 |
6,325 |
,000 |
-74,307 |
-45,693 |
|
2 |
1 |
26,000 |
6,182 |
,002 |
12,014 |
39,986 |
|
|
3 |
-34,000 |
7,024 |
,001 |
-49,889 |
-18,111 |
|
3 |
1 |
60,000 |
6,325 |
,000 |
45,693 |
74,307 |
|
|
2 |
34,000 |
7,024 |
,001 |
18,111 |
49,889 |
Based on estimated marginal means
* The mean difference is significant at the ,05 level.
a Adjustment for multiple comparisons: Least Significant Difference (equivalent to no adjustments).
Az összes lehetséges párosítás különbözik (a Sig. oszlopból leolvasható, hogy az 1 különbözik a 2-től is és a 3-tól is és a 2 is különbözik a 3-tól).
Végül, mivel ezt is bejelöltük, megrajzolja az átlagok grafokonját.
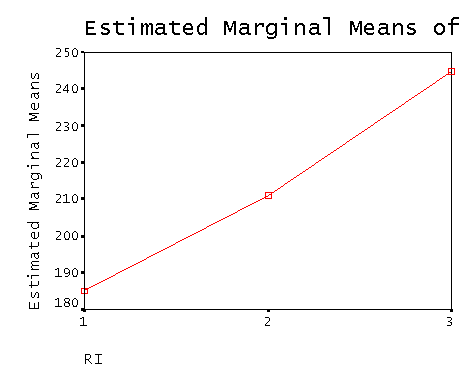
Az eredmény megadása
Eredményünk szerint az RI típusok szignifikánsan különböznek – F(2,18)=42,58 p< 0,01, a páros összehasonlítás szerint valóban a Donders által megadott ERI < SRI < VRI érvényes.
Kétszempontos variancia analizis független minták esetén
Ezt a próbát alkalmazzuk, amikor két független változó hatását vizsgáljuk a függő változóra. A függő változók két szempont több szintjén szerveződő csoportokat képeznek.. Például .érzelmi intelligenciát mérünk (függő változó) kisfiúk, kislányok, nők és férfiak csoportjaiban. Két független változónk a nem(nőnemű, hímnemű) és a kor(gyerek, felnőtt) és mindkettőnek két szintje van. Igy a varianciaanalízis sem egy F értéket szolgáltat, nem egy szempontra nézi, hogy van-e szignifikáns különbség, hanem kettőre. Két ún. főhatást kapunk, amelyek lehetnek szignifikánsak vagy sem – mindkettő szignifikáns, egyik sem, vagy az egyik szignifikáns, a másik nem. A két szempont használata maga után vonja azt a kérdést, hogy a függő változó ugyanúgy viselkedik-e a két szempont szintjein. Az előbbi példánál ez azt jelenti, hogy ha a nők érzelmi intelligenciája magasabb (szempont: nem), akkor ez csak a felnőttekre igaz vagy a gyerekekre is? Amennyiben a felnőttekre is és a gyerekekre is érvényes, akkor a függő változó a két szempont szintjein egyformán alakul. Ha viszont az egyik szempont szintjein kapott hatás nem érvényes, vagy ellentétesen alakul a másik szempont szintjein, akkor azt mondjuk, hogy a két szempont között interakció van. Nézzük meg hipotetiku adatokkal az eddigieket. Az ábrán látható a pontátlagok alakulása az egyes csoportoknál. Az ábráról az látható, hogy a hímneműek pontátlaga egy kicsit magasabb, mint a nőneműeké, a kor szempont szerint (gyerek, felnőtt) nem tiszta a kép. A varianciaanalízis azt mutatja, hogy a “nem” főhatás szignifikáns, a kor főhatás viszont nem szignifikáns. A két szempont szintjei közötti interakciót az mutatja, hogy a két görbe nem párhuzamos, hanem metszik egymást és ez itt nem véletlen, a varianciaanalízis szerint az interakció szignifikáns. Összefoglalva: a nem főhatás szignifikáns volta azt jelzi, hogy a hímneműek érzelmi IQ-ja magasabb, de ez a kor függvényében változik, gyerekeknél a lányok EQ-ja magasabb, míg felnőtteknél a férfiaké.
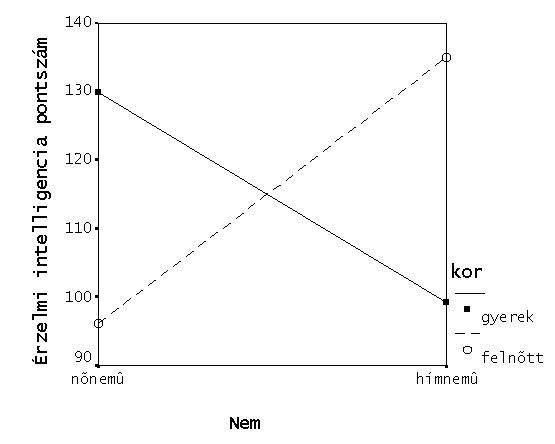
Példa
Az alvásdepriváció és az alkohol hatását vizsgáljuk a teljesítményre. Az utóbbit úgy mérjük, hogy egy videojátékban elkövetett hibák számát regisztráljuk. Azelrendezéa következő:
A két szempont: az alvás depriváció 3 szinttel (4 óra, 12 óra, 24 óra) és az alkohol 2 szinttel (van alkohol, nincs alkohol). Igy ez az elrendezés 3 × 2 = 6 csoportot igényel.
Alvás depriváció mértéke
4 óra 12 óra 24 óra
16 18 22
Alkohol van 12 16 24
17 25 32
11 13 12
Alkohol nincs 9 8 14
12 11 12
Adatok bevitele
Most 3 oszlopba kerülnek az adatok. Az egyik oszlopba az egyik szempont szintjei, a másik oszlopba a másik szempont szintkei, a harmadik oszlopba a mért értékek az alábbi minta szerint:
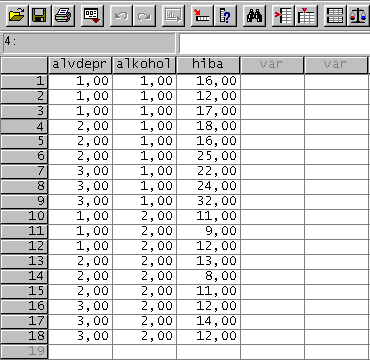
Érdemes a változókat kicsit átalakítani, mert a későbbiekben könnyebb lesz a táblázatok olvasása.
Ehhez kattints a képernyő bal alsó részén található Variable View fülre. Megjelenik a változók paramétereit tartalmazó táblázat, amelyben az egyes változók a sorokban találhatók. Az első változót (alvdepr) és a másodikat (alkohol) alakítsuk át a következő képpen:
A “Label” oszlopba írd be a változó nevét.
A “Values” oszlopba kattintva megjelenik egy újabb ablak, amit értelemszerűen (ld. alábbi ábra) tölts ki. Azaz, a “Value:” mellé írd be az első olyan értéket, amit a változó felvehet, alatta a “Value Label:” mellé írd be
azt, hogy ez mit jelent. Pl. az alkohol változó esetén az 1 érték azt jelenti, van alkohol fogyasztás, a 2 érték azt jelenti, hogy nincs.Most már csak az OK – ra kell kattintani és visszalépni az adatszerkesztőbe.
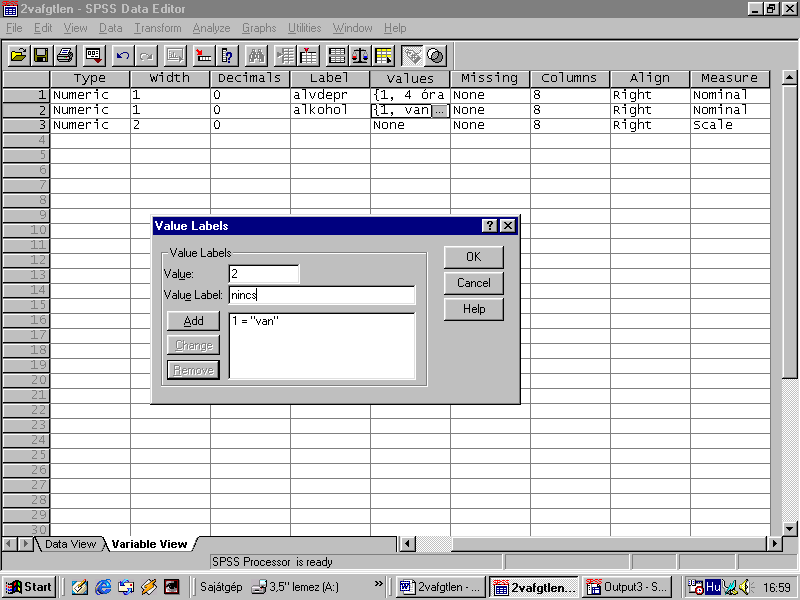
Az elemzés inditása
Analyze " General Linear Model " Univariate
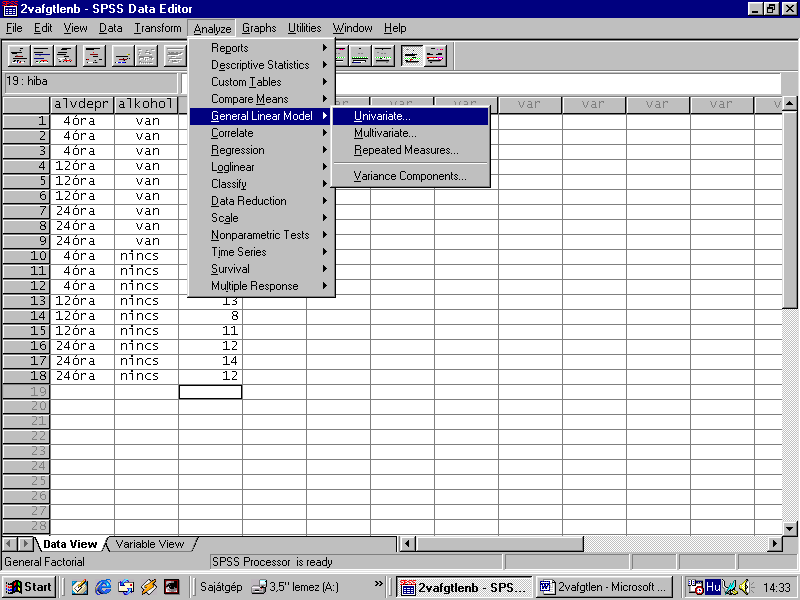
A jobboldali ablakból a függő változót (hiba) átrakjuk a Dependent Variable ablakba, majd megadjuk a független változókat (faktorokat) a Fixed Factor ablakba.
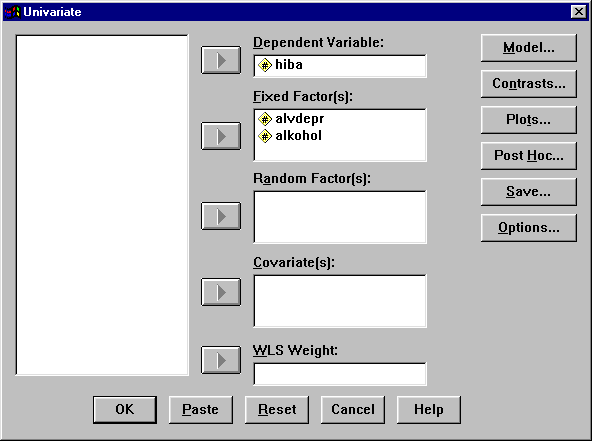
Most az Options… bekapcsolásával megadhatók a különböző lehetősé
gek.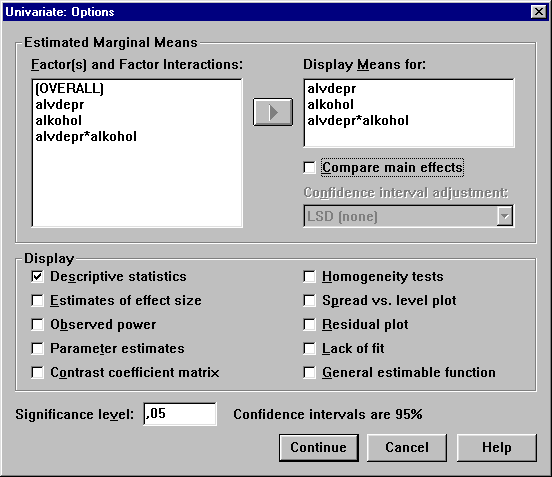
A Display oszlopban érdemes bejelölni a Descriptive statistics lehetőséget az alapstatisztikákhoz. Majd a Factor(s) and Factor Interactions: ablakban bejelöljük az alvdepr, az alkohol és az alvdepr*alkohol-t és a u
-ra kattintva betesszük a Display Means for: ablakba. Ekkor bekapcsolható a Compare main effect is.Continue után visszajön a főmenű, amiből a Plots-ra kattintva megadhatjuk a grafikon jellemzőit.
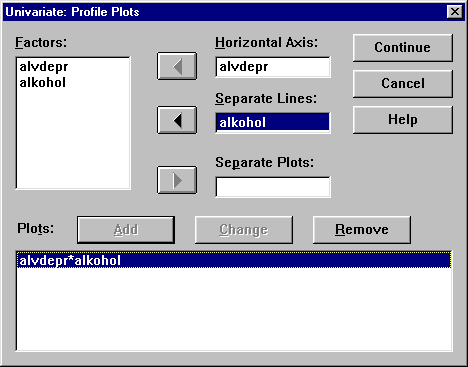
Ha ez készen van, akkor Continue és a visszakapott főmenűben OK.
Az eredmények:
Először a csoportok elrendezését kapjuk meg (itt derül ki, hogy az adatbevitel a szándékainknak megfelelően sikerült-e). Gyors ellenőrzés, valóban két szempontunk van (alvdepr és alkohol), az alkohol szerinti két csoportban 9-9 személy, az alvás depriváció sz
erinti 3 csoportban valóban 6-6 személy van.Between-Subjects Factors
|
|
|
Value Label |
N |
|
alvdepr |
1 |
4óra |
6 |
|
|
2 |
12óra |
6 |
|
|
3 |
24óra |
6 |
|
alkohol |
1 |
van |
9 |
|
|
2 |
nincs |
9 |
Ezután a leíró statisztikai adatok következnek a két szempontszintjei szerinti elrendezésben: átlag (Mean), szórás (Std. Deviation), elemszám (N). A Total feliratú sorban található átlag és szórás értelemszerűen az első esetben a 4 órás alvásdeprivációra vonatkozik (tehát egybe rakva az alkoholt kapott és alkoholt nem kapottakat), majd ugyanígy a 12 és
Descriptive Statistics
Dependent Variable:
|
alvdepr |
alkohol |
Mean |
Std. Deviation |
N |
|
4óra |
van |
15,00 |
2,65 |
3 |
|
|
nincs |
10,67 |
1,53 |
3 |
|
|
Total |
12,83 |
3,06 |
6 |
|
12óra |
van |
19,67 |
4,73 |
3 |
|
|
nincs |
10,67 |
2,52 |
3 |
|
|
Total |
15,17 |
5,98 |
6 |
|
24óra |
van |
26,00 |
5,29 |
3 |
|
|
nincs |
12,67 |
1,15 |
3 |
|
|
Total |
19,33 |
8,07 |
6 |
|
Total |
van |
20,22 |
6,10 |
9 |
|
|
nincs |
11,33 |
1,87 |
9 |
|
|
Total |
15,78 |
6,33 |
18 |
Ezután következik a varianciaanalízis eredménye (Tests of Between-Subjects Effects). A főhatások: ALVDEPR F= 5,79 p< 0,05, ALKOHOL F=31,68 p< 0,01. Az interakció: ALVDEPR*ALKOHOL F= 2,70 p>0,05. Azaz, mindkét főhatás szignifikáns (mind az alvásdepriváció mind az alkohol hat a hibára) és nincs interakció
Tests of Between-Subjects Effects
Dependent Variable:
|
Source |
Type III Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Corrected Model |
546,444 |
5 |
109,289 |
9,739 |
,001 |
|
Intercept |
4480,889 |
1 |
4480,889 |
399,287 |
,000 |
|
ALVDEPR |
130,111 |
2 |
65,056 |
5,797 |
,017 |
|
ALKOHOL |
355,556 |
1 |
355,556 |
31,683 |
,000 |
|
ALVDEPR * ALKOHOL |
60,778 |
2 |
30,389 |
2,708 |
,107 |
|
Error |
134,667 |
12 |
11,222 |
|
|
|
Total |
5162,000 |
18 |
|
|
|
|
Corrected Total |
681,111 |
17 |
|
|
|
a R Squared = ,802 (Adjusted R Squared = ,720)
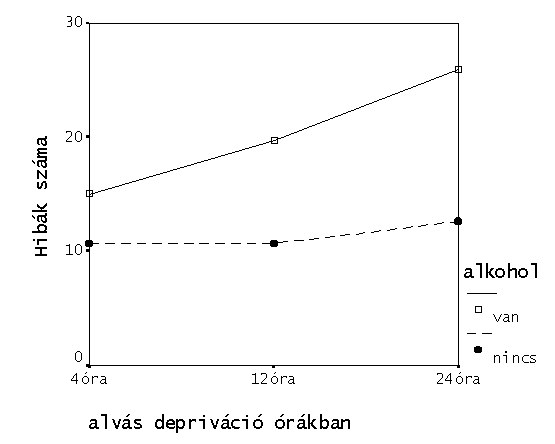
Mivel a Plot menűt bekapcsoltuk, egy ábrát is kapunk:
Ezt az eredmény ismeretében már jól tudjuk olvasni, a két görbe valójában párhuzamosnak tekinthető (mert nem szignifikáns az interakció), a két görbe valóban kettő, távol egymástól (az ALKOHOL szignifikáns) és mindkét görbe – azért mindkettő, mert nincs interakció) az alvásdepriváció növekedésével emelkedik, azaz nő a hibák száma.
Multiple Comparisons
Dependent Variable:
Bonferroni
|
|
|
Mean Difference (I-J) |
Std. Error |
Sig. |
95% Confidence Interval |
|
|
(I) alvdepr |
(J) alvdepr |
|
|
|
Lower Bound |
Upper Bound |
|
4óra |
12óra |
-2,33 |
1,93 |
,753 |
-7,71 |
3,04 |
|
|
24óra |
-6,50 |
1,93 |
,017 |
-11,88 |
-1,12 |
|
12óra |
4óra |
2,33 |
1,93 |
,753 |
-3,04 |
7,71 |
|
|
24óra |
-4,17 |
1,93 |
,157 |
-9,54 |
1,21 |
|
24óra |
4óra |
6,50 |
1,93 |
,017 |
1,12 |
11,88 |
|
|
12óra |
4,17 |
1,93 |
,157 |
-1,21 |
9,54 |
Based on observed means.
* The mean difference is significant at the ,05 level.
Pairwise Comparisons
Dependent Variable:
|
|
|
Mean Difference (I-J) |
Std. Error |
Sig. |
95% Confidence Interval for Difference |
|
|
(I) alkohol |
(J) alkohol |
|
|
|
Lower Bound |
Upper Bound |
|
van |
nincs |
8,889 |
1,579 |
,000 |
5,448 |
12,330 |
|
nincs |
van |
-8,889 |
1,579 |
,000 |
-12,330 |
-5,448 |
Based on estimated marginal means
* The mean difference is significant at the ,05 level.
a Adjustment for multiple comparisons: Least Significant Difference (equivalent to no adjustments).